Формулы расчета процентов по вкладу — простой и сложный процент

Основная цель обращения клиента, у которого есть сбережения, в банк заключается в том, чтобы сохранить и приумножить денежные средства. Чтобы выбрать из большого ассортимента предложений различных организаций наиболее выгодный вариант, нужно самостоятельно уметь рассчитывать будущую доходность вложений. Зачастую, варианты, которые на первый взгляд кажутся самыми выгодными и интересными, не приносят хорошего результата. Поэтому нужно уметь прогнозировать проценты по вкладу до совершения сделки.

Для расчетов доходности по вкладу используется простой и сложный методы начисления процентов. Каждый из них имеет свои особенности и «подводные камни», которые стоит учитывать. Рассмотрим подробнее, как пользоваться формулами для расчета процентов по вкладу, что означает каждая составляющая, и посчитаем на примерах эффективность каждого метода.

Формулы начисления процентов.

Доходность практически любого вклада можно рассчитать самостоятельно, зная методику расчета. Для этого нужно знать параметры будущего вложения, к которым относится:

• Депозитная сумма.
• Ставка (в %).
• Периодичность процентного начисления.
• Срок размещения денег.

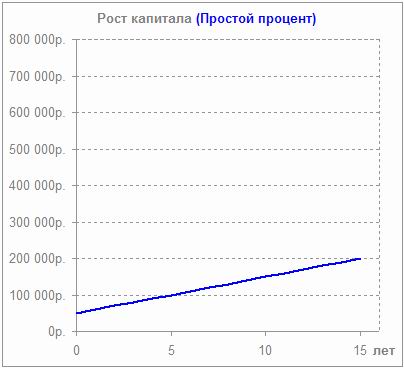
Формула простых процентов.

Она используется тогда, когда начисляемый доход присоединяется к основному телу депозита в конце его срока или не присоединяется и выводится на текущий счет или пластиковую карточку. Этот порядок расчета стоит учесть, когда размещается солидная сумма на длительный срок. Обычно в данном случае банки применяют варианты размещения без капитализации, что понижает общую выгоду вкладчика.

Формула простого %:

Сумма % — это доход, полученный через i-ый промежуток времени.

Р – изначальный объем вложений.

i – депозитная годовая ставка.

t – срок вложения.

T – число дней в году.

Рассмотрим пример: разместим 100 000 рублей на полгода под 12%. Рассчитаем полученный доход:

Таким образом, через полгода со счета можно будет снять 105 950,68 руб.

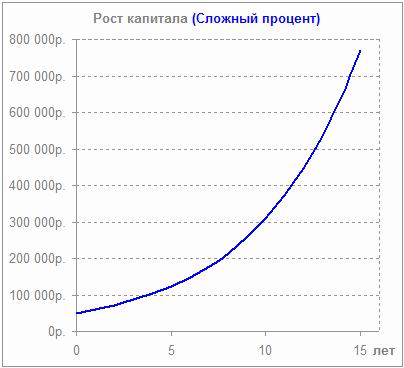
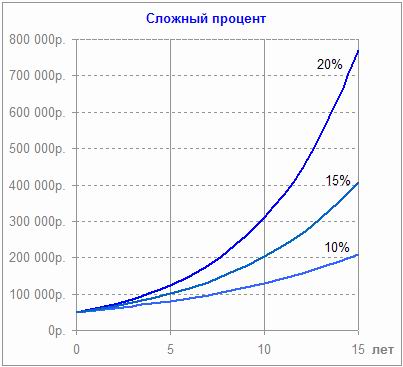
Формула сложных процентов.

Она применяется реже в депозитной практике банка, но такие предложения найти можно. Для большинства вкладчиков они не являются привлекательными по причине того, что ставки по ним ниже, чем по продуктам, когда доход начисляется только по окончании действия депозитного договора. Периодичность присоединения дохода может быть разной: раз в месяц, раз в неделю, раз в квартал, каждый год. Она подразумевает под собой капитализацию или начисление «процентов на проценты».

Формула сложных %-ов:

P – изначальная сумма вклада.

i – депозитная годовая ставка.

k – число дней в периоде, через который начисляется доход.

T – число дней в году.

n – число капитализаций дохода в течение всего срока депозита.

Рассмотрим пример №1: разместим 100 000 рублей под 12% годовых на полгода с ежемесячной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Таким образом, благодаря ежемесячной капитализации, общий итог вложений оказался выгоднее, чем в варианте, когда проценты причисляются в конце срока.

Пример №2: разместим 100 000 рублей на 6 месяцев под 12% годовых с еженедельной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Пример №3: разместим 100 000 рублей на 1 год под 12% годовых с ежеквартальной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Пример №4: разместим 100 000 руб на 1 месяц под 12% годовых с ежедневной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Таким образом, капитализация и формула сложных процентов дает более выгодный эффект, поэтому, при размещении денег в банке не стоит упускать из виду подобные варианты размещения.

Простые и сложные проценты по вкладам

Выгода банковского вклада оценивается не только по процентной ставке. Большое влияние на доходность депозита оказывает способ начисления процентов. В финансовой сфере существует понятие простого и сложного процента. Когда применяется тот или иной метод расчета? Как осуществляется начисление процентов по каждому способу? И какой метод выгоднее для вкладчика?

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем.

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S – сумма насчитанных процентов (руб.);

P – начальная сумма вложенных средств;

I – процентная ставка за год;

Т – срок действия вклада в днях;

K – число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовых вычисление простых процентов будет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Как рассчитать сложный процент по вкладу

В отличие от простой ставки процентов, сложная начисляется на постоянно растущую основу с учетом процентов, которые начислены за предыдущие периоды. Иными словами проценты, полученные за определенный период (неделю, месяц, квартал год) прибавляются к начальной сумме вклада (капитализируются). А в следующем периоде они начисляются уже на всю эту сумму вместе, и так каждую неделю, месяц или квартал.

Выходит, что в отличие от модели простых процентов, основа для начисления сложных будет расти с каждым новым периодом. Ведь главная суть расчетов состоит в том, что выполняется начисление процентов на процент.

Если метод простых процентов основывается на арифметической прогрессии, то сложных – на геометрической. Формула их расчета выглядит таким образом:

S = (P x I x J / K) / 100, где:

S – сумма насчитанных процентов (руб.);

P – начальная сумма вложенных денег;

I – процентная ставка за год;

J – период, за который проводится капитализация (дней);

K – число дней в году.

Например, при первоначальном вкладе 100 000 руб. под 10% с учетом ежемесячной капитализации за первый месяц (допустим, март) вкладчик получит:

• (100 000 х 10 х 31 / 365) / 100 = 849,32 (руб.);
• после эта сумма добавляется к начальному вкладу (происходит капитализация): 100 000 + 849,32 = 100 849,32 (руб.);
• аналогичным способом высчитывается доход за апрель: (100 849,32 х 10 х 30 /365) / 100 = 828,90 (руб.);
• после чего опять производится ежемесячная капитализация: 100 849,32 + 828,90 = 101 678,22 (руб.);
• далее – за май: (101 678,22 х 10 х 31 /365) / 100 = 863,57 (руб.);
• после очередной капитализации у вкладчика на счете получается сумма: 101 678,22 + 863,57 = 102 541,79 (руб.);
• и так до конца срока депозита.

Чтобы увидеть эффект метода сложных процентов, нужно сравнить полученную сумму (102 541,79 руб.) с суммой, определенной путем расчета простых процентов (102 520,55 руб.) при тех же условиях (100 000 руб. под 10% на 3 месяца).

Получается, что во втором случае величина прибыли немного больше. При этом существует прямая зависимость: чем больше срок вклада, тем больше разница в доходах, рассчитанных разными способами.

В каких случаях используется начисление простых и сложных процентов?

Формула простых процентов по вкладам применяется, когда полученные проценты плюсуются к телу депозита лишь в конце периода или совсем не прибавляются, а переводятся на другой счет. Формулу сложных процентов используют, когда проценты насчитываются через равные временные промежутки (месяц, квартал, год). Это означает проведение капитализации процентов (когда проценты насчитываются на проценты).

Простые проценты используются в случаях оформления краткосрочных вкладов, период действия которых, в основном, меньше года. Метод сложных процентов применяется при долгосрочных вкладах, которые открываются на срок больше года.

Сравнение методов сложных и простых процентов

Хранение денег в банке с целью увеличения собственных накоплений называется наращением. Даже при самом упрощенном примере начисление процентов происходит один раз в год. Поэтому через год вкладчик закрывает депозит и забирает всю сумму плюс начисленные проценты.

Наращение по простым процентам определяется согласно формуле:

S = P (1 + ni), где:

P – начальная сумма вложенных денег;

n – количество этапов начисления процентов;

i – процентная ставка.

Величина (1 + ni) на языке финансистов называется множитель наращения простых процентов. Она показывает, во сколько раз наращенная сумма превышает изначальную.

Наращенную величину можно также представить в виде суммы:

S = P+ I, где:

P – первоначальная сумма вложенных денег;

I = Pni – сумма процентов.

Пример. Положив депозит в сумме 200 000 руб. под 12% годовых на полгода, клиент получает такую сумму процентов:

I = Pni = 200 000х0,5х0,12 = 12 000 (руб.);

и наращенную величину:

S = P+ I = 200 000+12 000 = 212 000 (руб.).

Величина, обратная наращению, называется дисконтирование по простым процентам. Она определяет сегодняшнюю стоимость будущей денежной суммы. Этот показатель дает возможность определить, сколько сегодня будут стоить средства, которые получит вкладчик в будущем.

Ставка дисконтирования, которая используется в расчетах, учитывает такие риски, как инфляция, изменение ставки или нормы доходности. У банков, имеющих высокую степень надежности, таких, как Сбербанк, ставка дисконтирования находится в пределах процентной ставки.

В отличие от начисления простых процентов, формула наращения по сложным процентам представляется так:

S = P (1 + i/ny) nd , где:

P – первоначальная сумма вложенных денег;

i – процентная ставка;

ny – количество циклов капитализации на протяжении года;

nd– количество циклов капитализации за все время депозита.

Здесь множителем наращения является выражение (1 + i/ny) nd , а сам метод основан на законе геометрической прогрессии.

Пример. При вложении 200 000 руб. с ежеквартальной капитализацией на полгода наращенная сумма вклада составит:

S = P (1 + i/ny) nd = 200 000 (1+0,12/4) 2 = 200 000х1,03 2 = 200 000х1,0609 = 212 180 (руб.).

Если этот же пример рассчитать с учетом ежемесячной капитализации, получится:

S = P (1 + i/ny) nd = 200 000 (1+0,12/12) 6 = 200 000х1,01 6 = 200 000х1,0615 = 212 300 (руб.).

Простая и сложная ставка процентов: какие вклады выгоднее?

Из описанных примеров становится понятно: чем больше множитель наращения, на который будет умножаться сумма депозита, тем больше получится наращенный доход по вкладу.

Чтобы более наглядно продемонстрировать разницу по использованию простой схемы начисления процентов и сложной, данные занесены в таблицу:

При подсчете коэффициентов использовалась ежегодная капитализация процентов. Из таблицы видно, что:

• если срок вклада меньше года, то множитель, рассчитанный по формуле простых процентов, получается больше. Это даст возможность вкладчику получить больший доход, чем при использовании сложных процентов;
• когда период вклада составляет 1 год – величина коэффициентов сравнивается и является одинаковой. Это говорит о том, что доход с ежегодной капитализацией при начислении по простым процентам и сложным будет равный;
• если срок депозита более года, то коэффициент наращения по сложным процентам выше, чем при использовании обыкновенного простого процента.

Составив аналогичную таблицу с учетом проведения ежеквартальной капитализации, можно увидеть, что доход будет одинаков при вкладе на квартал. При более коротких депозитах (на месяц или два) больший доход будет получаться по простым процентам. При вкладах на срок более квартала, наоборот, выгоднее будут сложные проценты.

Этот принцип определения доходности вклада зависимо от метода вычисления процентов сохраняется и при расчетах на месяц. Подведя итог, можно сказать, что применение сложного процента выгодно, если период вклада превышает период капитализации. Иначе говоря:

• при ежегодной капитализации оформление депозита выгодно, если срок его действия больше года;
• с применением ежеквартальной капитализации сложные проценты будут выгодными только тогда, когда срок действия депозита больше 3 месяцев;

Если срок депозита меньше, чем периодичность проведения капитализации, то расчет простых процентов по вкладам получится выгоднее.

Источник https://investor100.ru/formuly-rascheta-procentov-po-vkladu/

Источник https://cbkg.ru/articles/prostye_i_slozhnye_procenty_po_vkladam.html

Источник

Источник