Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1

Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?

Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?

Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.

Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов

Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.

На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?

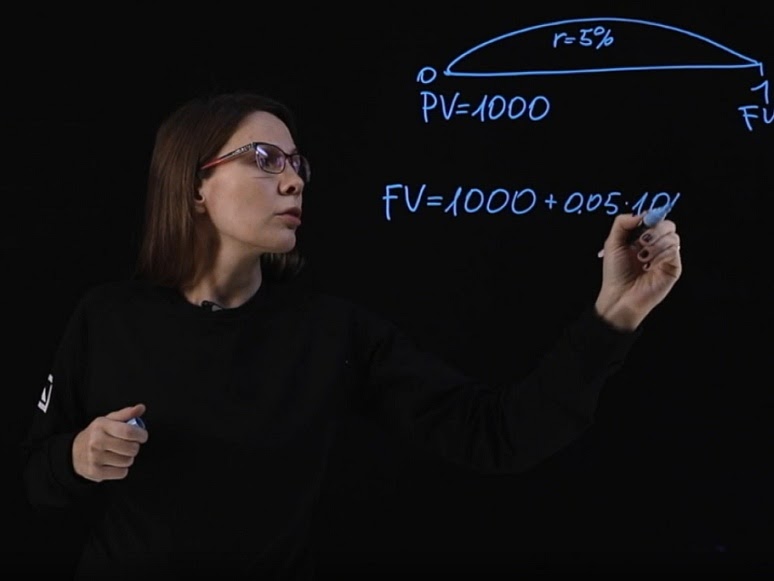
Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.

На языке математики это будет выглядеть так:

Сейчас вы мне даете тысячу рублей. Обозначим это как PV (Present Value) . Допустим ставка (r) равна 5%, и деньги вы даете мне сроком на один год. Тогда возвращая деньги FV (Future Value) , мне придется добавить к исходной сумме 50 рублей.

Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.

Простые проценты

Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:

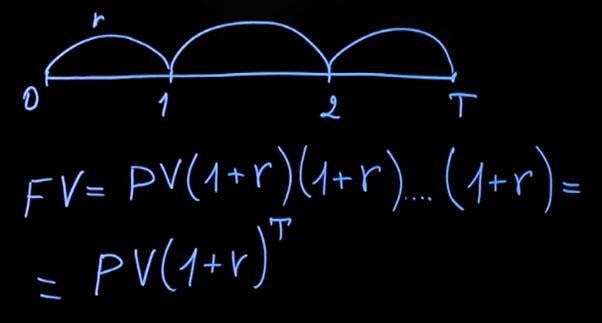
Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.

Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.

Непрерывное начисление процентов

Давайте рассмотрим, как будет выглядеть формула для начислений процентов чаще одного раза в год. В этом случае будущее значение будет равняться текущему значению, умноженному на сумму единица плюс годовая процентная ставка, деленная на количество периодов начислений в году (n) в степени nT . Если начисления производятся каждые полгода, то n=2 , если каждый день, то n=365 .

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:

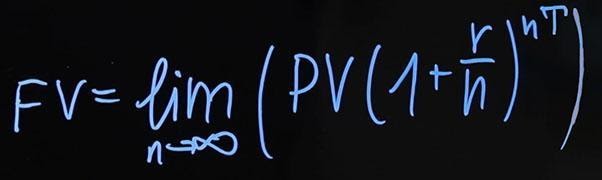
Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:

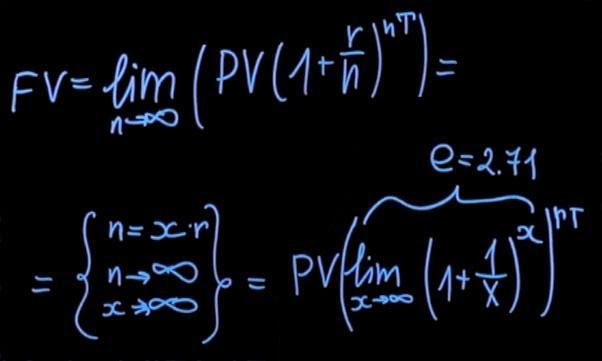
С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.

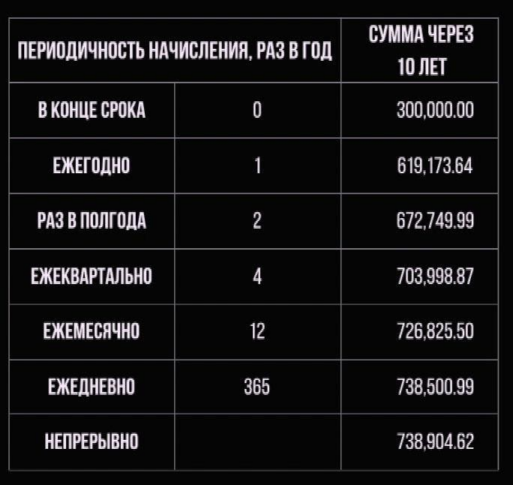
Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.

На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.

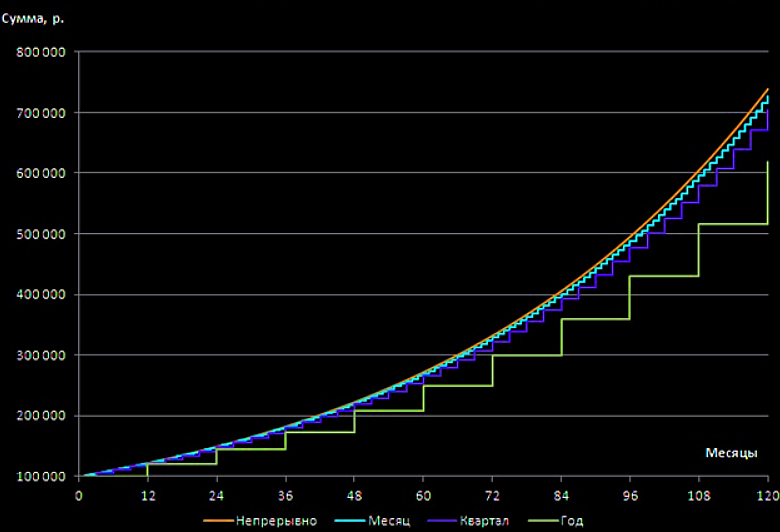
Отсюда необходимо сделать вывод:

Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.

#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)

Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.

Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?

Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:

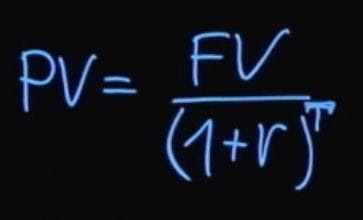
T – это количество периодов выплат начислений процентной ставки. Такой процесс деления будущего значения на единицу плюс процентная ставка в степени T называется дисконтированием. А множитель, единица деленная на сумму единицы плюс r в степени T , называется коэффициентом дисконтирования.

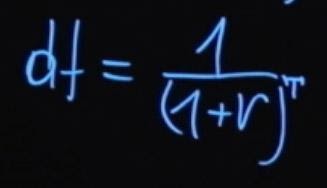
Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.

Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.

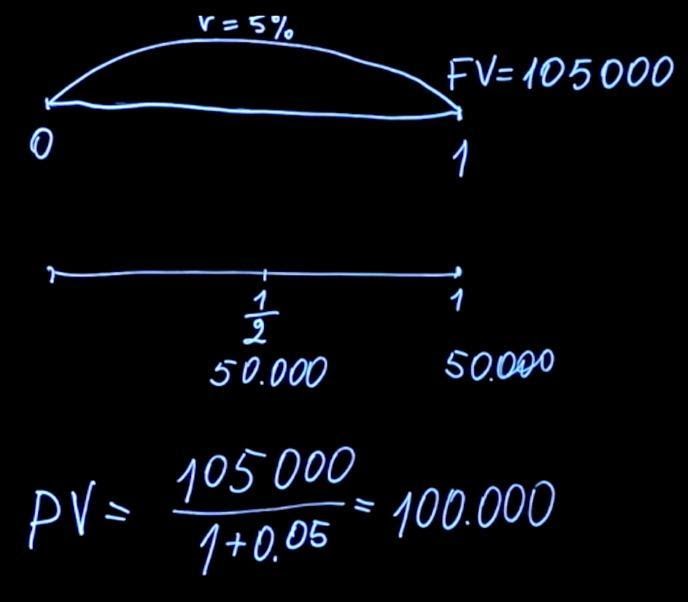
Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.

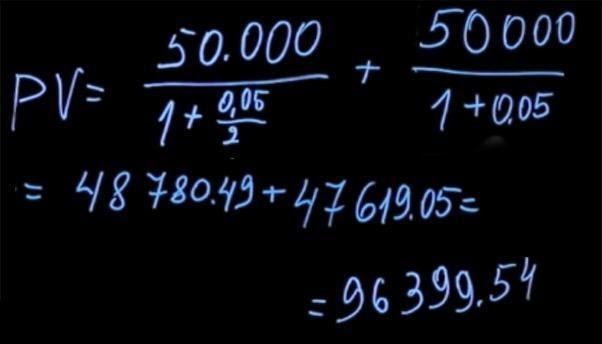
В таком случае сравнение будет корректным.

#3. Форвардные процентные ставки

Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Мы находимся сейчас в моменте времени «ноль». Через год я у вас по ставке x возьму деньги и верну их вам через два года. Как рассчитать ставку x ? У нас есть несколько опций. Вы можете сейчас положить деньги по ставке r ₁ на год, а затем реинвестировать их по ставке x .

Либо положить деньги сразу по ставке r ₂ на два года.

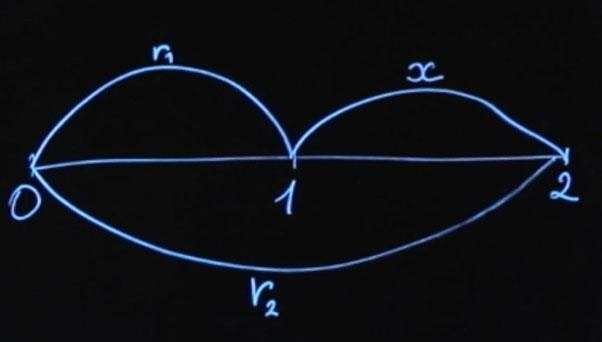
На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV ₁ будет равняться текущему значению, умноженному на сумму единицы и rT ₁ (будем считать, что у нас простое начисление процентов).

Момент времени T ₁ у нас равняется одному году. Дальше у нас произойдет реинвестирование суммы, и мы положим на промежуток времени от T ₂— T ₁, умноженную на нашу процентную ставку x . T ₂ – это момент времени, в нашем случае два года.

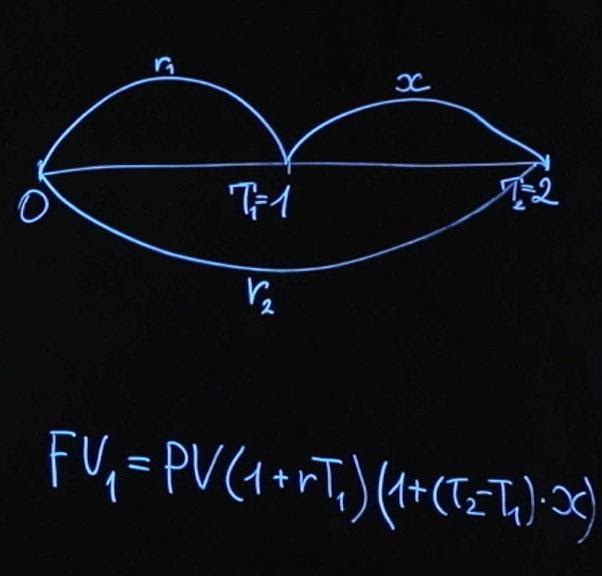
Либо будущее значение FV ₂ будет равняться текущему значению PV , умноженному на единица плюс r ₂, умноженное на T ₂. Согласно условию отсутствия арбитража FV ₁ должно равняться FV ₂.

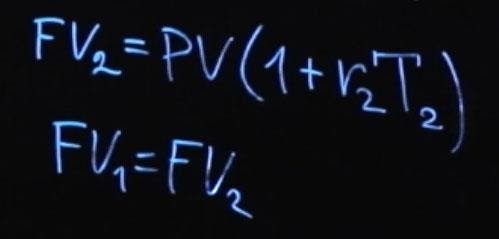
Из этого мы получаем следующее:

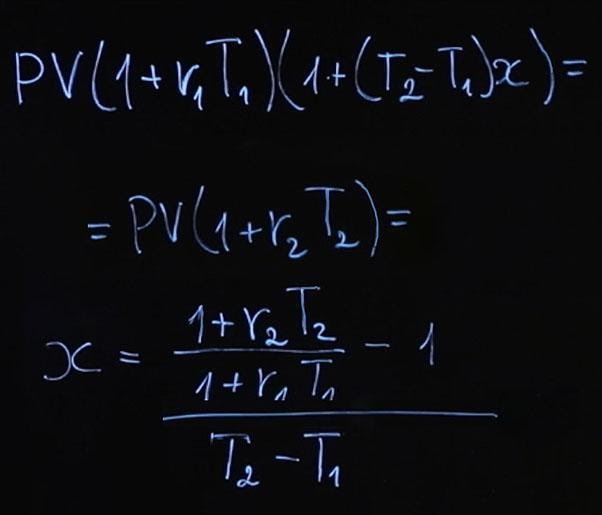
Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.

Пусть процентные ставки у нас r ₁=4%; r ₂=6%. В таком случае имеем следующее:

Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.

Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:

Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:

Далее легко найти x:

Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.

Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?

Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.

Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T₁. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.

Инвестиционный калькулятор онлайн: определение виды инструкция

Инвестиционный калькулятор онлайн. Единственный способ обеспечения финансовой независимости это пассивный доход. Создать можно грамотно выкладывая средства. Если принято решение накапливать деньги и заниматься долгосрочными инвестициями. То придется делать фундаментальные вычисления и корректировки в процессе инвестиционного периода.

Хотите рассчитать другие данные. Просто обновите страницу нажав на клавиатуре F5

Инвесторы, а особенно начинающие должны уметь высчитать выгодность капиталовложений. Для этого пригодится инвестиционный калькулятор онлайн.

Разновидность финансового инструмента, где можно посчитать простой процент, сложный, денежный поток, возможную прибыль при определенном начислении. Незаменимая вещь инвестора. С его помощью можно определить будущий размер денежных средств, через определенный промежуток времени. Под конкретные начисления и при регулярном пополнении. Подобные вычисления можно сделать и на обычном калькуляторе. Но сделать это сложнее и займет больше времени. К тому же необходимо обладать математическими знаниями. Ведь доходность меняется в некоторых случаях ежеквартально (американские компании).

Лучший финансовый инструмент для инвестора — Инвестиционный калькулятор онлайн

Инвестиционный калькулятор онлайн, рассчитать на котором можно доход, стартовую сумму и время необходимое для накопления.

Его преимущество в том, что он предоставляет разные типы расчетов:

— вычисление дохода (показывает итоговые результаты капиталовложений). Иными словами, на какой капитал можно рассчитывать спустя определенное время;

— вычисление стартового капитала (показывает какую начальную сумму потребуется вложить для достижения поставленной цели);

— вычисление времени инвестирования (показывает какое время, потребуется для достижения цели).

Пользоваться просто и самое главное быстро. Инвестиционный калькулятор представляет собой специальные окошки, где необходимо указать:

1. Начальные средства. Количество денег, планируемое для инвестирования на первом этапе. От этого зависит многое: период инвестирования, конечные цифры, финансовая свобода.

2. Срок инвестирования. Промежуток в течение которого планируется достичь определенного числа денег. Ежегодно оно растет в геометрической прогрессии. Это нелегкое время, где придётся себя ограничить. Но со временем это окупится сполна и не придется переживать о финансах.

3. Ставка. Годовая прибыль в процентном выражении. К сожалению эта величина не бывает абсолютно точной. На это влияют множество факторов. Даже в банковском вкладе нельзя быть уверенным в стабильных будущих значениях. Для более точного подсчета, желательно указывать чуть сниженный доход инвестиций.

4. Дополнительные вложения или месячная прибавка. Это деньги стабильно вносимые на инвестиционный счёт, например, с заработной платы. От этого будет зависеть насколько быстро достигните финансовой независимости и свободы.

5. Период реинвестирования.

Заполнив указанные поля, кликаем на кнопку, обычно она обозначается «рассчитать». Результат выдаётся таблицей, либо списком с указанием итогового капитала по месяцам, годам и общей прибылью за весь период.

Стоит упомянуть! Если деньги уже генерируют прибыль и она ежемесячно изымается, то с помощью калькулятора можно узнать, растут капиталовложения или сокращаются в течение оставшегося времени инвестирования.

Он имеет специальное окошко с названием «регулярные до вложения». Прописываем в нем стабильно снимаемую сумму. Указывать в окошке следует со знаком минус (-).

Консультация или гарант

Люди ошибочно считают, что калькулятор даёт гарантированную доходность. Он предоставляет лишь примерный расчёт и носит исключительно информационный и консультационный характер. Задача показать ожидаемый приблизительный итог.

Калькулятор не может предсказать или предусмотреть возможные колебания рынка. Кризисные моменты, в результате которых дивиденды могут быть понижены или вовсе отменены, а котировки акций значительно просесть. Но примерную картину он покажет.

Благодаря инвест инструменту можно получить данные:

— узнать потенциал инвестиций с учётом регулярных пополнений и капитализацией;

— узнать реальную прибыль по инвестициям или вкладам;

— рассчитать доходность от инвестиций с учётом стабильных вложений и сложного процента.

Учёт сложного процента

Полезных инструментов сегодня много. Таким является инвестиционный калькулятор сложный процент. Сложная доходность, простым языком: полученная прибыль уходит в тело вклада и следующие начисления получаются уже от больших средств, так как тело увеличилось.

Это можно сравнить со снежным комом, который нарастает по мере движения. Альберт Эйнштейн назвал эго величайшим открытием современности. Некоторые называют восьмым чудом света и это действительно так.

Даже без регулярных вложений, можно достичь просто фантастических чисел на длинной дистанции. По сути, это реинвестирование. Полученную прибыль, в нашем случае дивиденды, вкладываем снова в акции. Тем самым растет размер инвестиций, а вместе с ним начисляемые на вложенные деньги проценты.

На начальном этапе этот эффект малозаметный. Но спустя десять или двадцать лет, итоговый размер капитала поистине впечатляет. Чтобы это понять и так сказать заглянуть в будущее, рассмотрим на примере. Для этого нам потребуется, как раз, инвестиционный калькулятор сложных процентов.

Расчет доходности за 10 лет

В качестве примера, возьмём инвестирование в фондовый рынок. Чтобы узнать какое количество денег можно ожидать спустя 10 лет. При стабильном увеличении счета на 10 000 рублей, под 15% в год.

Переходим к заполнению:

1. Стартовый капитал – 10 тысяч рублей.

2. Период инвестирования – 10 лет.

4. Регулярные до вложения в размере – 10 000.

5. Период реинвестирования раз в год.

Нажимаем на кнопку «рассчитать» и получаем общее число пополнений 1.2 млн рублей. Доход 1 434 407 руб., итоговая сумма 2 644 407 рубля. Деньги за десять лет увеличились в два раза.

На инвестиционном калькуляторе с реинвестированием и пополнением можно посмотреть итог получившийся за 20 лет. Мы получаем общее количество 15 159 549 рублей. Тут уже начинаешь понимать, о действительно мощной силе феномена. Вкладываем 2.4 млн руб., а увеличиваем деньги на 531% или в пять раз.

Повторюсь, подсчет примерный. Инвестиционный калькулятор онлайн сложные проценты, может послужить неплохим мотиватором начала инвестирования. Многие начинающие инвесторы, бросают инвестирование, считая невозможным достичь хорошего состояния при небольших стабильных пополнениях. Но расчеты говорят об обратном.

Инвестиции это математика и деньги любят счет. Мы разобрали универсальный финансовый инструмент или инвестиционный калькулятор с реинвестированием. Реинвестирование это направление начисленных процентов в тело вклада. На полученные дивиденды докупаем акции. Тем самым капитал увеличивается, и начисления будут уже от большей суммы. Даже реинвестируя небольшие деньги, эффект получится отличный.

Полезно! Как получать дивидендами 50 тысяч рублей ежемесячно? Обратимся к книге «Финансовая независимость» Бодо Шеффера. В ней приводится полезная и простая формула. Желаемую сумму (50 000) умножаем на 150 и получаем деньги, необходимые для генерации «дивидендной зарплаты». 50 000*150=7 500 000. Значит необходимо накопить 7.5 миллионов руб.

Как и за сколько можно накопить

Как и за сколько можно накопить такое количество денег? В этом нам поможет инвестиционный калькулятор онлайн с реинвестированием дивидендов.

Приступаем к заполнению:

1. В окошке «вычислить» выбираем «Стартовый капитал».

2. Наша цель 7.5 млн.

3. Срок инвестирования выбираем 20 лет.

4. Ставка 15%. Вполне реальный процент на фондовом рынке. В 2020 году НЛМК выплатил более 20% в год.

5. Ежемесячные вложения 10 000. На калькуляторе есть возможность выбора дополнительных вложений (раз в год).

6. Период реинвестирования — раз в полгода. Примерно так начисляются дивиденды. Большинство российских компаний начисляют дивиденды один раз в год. Американцы осуществляют начисления ежеквартально. Также есть возможность выбора периодичности: раз в месяц, в квартал и раз в год. Можно выбрать и без ре инвеста.

7. Щелкаем на вкладку «Рассчитать».

Итог получившийся за 20 лет

Ниже мы видим, что за 20 лет вложим 2.4 млн, доходность при текущей ставке составит 5.49 млн рублей. А начальные капиталовложения составляют 389 тысяч. Как видите, вполне реально скопить 7.5 миллионов и жить на дивиденды.

Рассмотрим подробнее выпадающий список с результатами. Нас интересуют ежемесячные результаты (нажав на «+»). Первые полгода начислений нет. Только рост средств вложений, а вот на седьмой уже появляются проценты. Это связано с тем, что «ре инвест» мы делаем раз в полгода. Начисленные проценты от инвестиций, направляются в общую сумму спустя это время. Конечно результат будет лучше, если реинвестировать чаще. Но таких дивидендов нет. Самый короткий срок раз в квартал.

Полезно! Чтобы узнать, через какое время денежные вложения будут удваиваться, необходимо разделить 72 на процентную ставку.

Например, мы инвестируем под 8% в год. Значит 72÷8=9. Потребуется девять лет для увеличения денег вдвое и спустя каждые девять лет они будут удваиваться. С помощью этой формулы можно сделать и обратный расчет, т.е. когда деньги обесценятся. Это касается тех, кто хранит деньги под подушкой. Годовой процент инфляции делим также на 72 и получаем количество лет. К примеру, если инфляция составляет 7%, то 72÷7=10.2. Спустя десять лет и два месяца деньги обесценятся вдвое.

Время затраченное для накопления

На калькуляторе также можно подсчитать, какое время потребуется для достижения определенного капитала. Например, вы хотите накопить на счету 7.5 млн. Для этого:

1. Во вкладке «Вычислить» выбираем «Срок достижения цели».

2. Целью оставляем все те же 7.5 миллионов. Вы можете вставлять свои значения.

3. А вот начальную сумму выберем 100 тысяч.

4. Ставка – 15% в год.

5. Дополнительные вложения – 10 000.

6. Реинвестирование раз в полгода.

7. Кликаем на «Рассчитать».

Получаем, что вложения составят 2 010 000 руб. Доход 7 500 000 и времени уйдет 16.9 лет, а если выбрать ре инвест раз в квартал, то срок уменьшится на три месяца. Повышая процентную ставку, потребуется ещё меньше времени.

Рассмотрим подробнее годовой результат. В первый год общее инвестиций составит 220 тысяч рублей (100 000 начальная сумма и 120 тысяч до вложения). Уже в первый год процентный доход будет равен 23 953 руб., второй 46 355 руб., а на третий 72 244 рублей и т.д. Как мы видим, деньги наращиваются стремительно. Понятно, что ключевую роль играют пополнение в виде 10 000 руб. Но и сложный процент делает своё дело.

Расчеты можно сохранить и просматривать во вкладке «Мои расчеты», которая находится в верхнем правом углу. Воспользуйтесь инструментом абсолютно бесплатно на нашем сайте. На сайте представлены и другие полезные инструменты.

2020 год буквально содрогнулся весь мир и изменил обыденное течение жизни, заставив многих задуматься о создании пассивного дохода. Кризис оставил немало людей без средств на существование, несовершенство пенсионной системы привело к повышению пенсионного возраста.

Высокий уровень инфляции и многое другое стало причиной массового потока людей на фондовый рынок. Только в 2020 году было открыто 7 миллионов брокерских счетов на Московской бирже. Постепенно люди начинают брать ответственность в свои руки за своё будущее.

Безусловно инвестируя мы рискуем своим капиталом. Однако, если объект подвергается тщательному анализу и расчету, то бояться нечего, а деньги начнут работать на вас.

Источник https://habr.com/ru/company/dbtc/blog/501566/

Источник https://kredit-cmotry-tyt.ru/investicionnyj-kalkuljator/

Источник

Источник